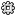기본적인 수식 삽입 방법 ¶
수식은 크게 두 가지 종류로 삽입이 되는데 하나는 작성중인 문장 사이에 inline으로 들어가는 수식이 있고, 수식 자체가 한 단락을 차지하도록 넣을 수도 있다. 문장 사이에 수식을 넣을 경우 해당 수식을

'\('와 '\)'로 감싸거나 '$'로 감싸준다. 단락으로 수식을 넣을 경우 '\['와 '\]'로 수식을 감싸준다.
임의의 직각삼각형에 대해 빗변의 길이를 \(c\), 나머지 두 변의 길이를 $a$, $b$로 나타내면 다음과 같은 관계가 항상 성립한다.
\[a^2 + b^2 = c^2\]
\[a^2 + b^2 = c^2\]

[PNG image (13.78 KB)]
복잡한 수식의 작성 ¶
수식에 번호를 삽입 하거나 여러 줄로 구성된 수식 단락을 삽입하고자 한다면 그에 맞는 수식 환경을 사용해야 한다. 대표적으로 사용되는 환경은 align 환경이다. 이 환경은 amsmath 패키지를 불러오면 사용이 가능하다.

폐구간 $[a,b]$에서 연속이고 개구간 $(a,b)$에서 미분 가능한 두 함수 $f$, $g$에 대해 미적분학의 기본 정리로부터 다음과 같은 관계를 얻는다.
\begin{align}
f(b)g(b) - f(a)g(a)
&=\int_a^b \frac{d}{dx} ( f(x) g(x) ) \, dx \nonumber\\
&=\int_a^b f'(x) g(x) \, dx + \int_a^b f(x) g'(x) \, dx.\label{intByParts}
\end{align}
식 \eqref{intByParts} 우변의 두 번째 항에 대해 정리하면 다음과 같은 부분적분 공식을 얻는다.
\begin{align*}
\int_a^b f(x) g'(x)\,dx = \left[ f(x) g(x) \right]_{a}^{b} - \int_a^b f'(x) g(x)\,dx.
\end{align*}
\begin{align}
f(b)g(b) - f(a)g(a)
&=\int_a^b \frac{d}{dx} ( f(x) g(x) ) \, dx \nonumber\\
&=\int_a^b f'(x) g(x) \, dx + \int_a^b f(x) g'(x) \, dx.\label{intByParts}
\end{align}
식 \eqref{intByParts} 우변의 두 번째 항에 대해 정리하면 다음과 같은 부분적분 공식을 얻는다.
\begin{align*}
\int_a^b f(x) g'(x)\,dx = \left[ f(x) g(x) \right]_{a}^{b} - \int_a^b f'(x) g(x)\,dx.
\end{align*}

[PNG image (37.24 KB)]
- 수식 작성을 위한 연습문제가 이 링크에 있다.